Master 1
La description des différents parcours du M1 ACSYON et des contenus des modules se trouvent ci-dessous.
Quatre parcours possibles pour l'inscription en première année
Cliquez sur le parcours pour une description détaillée :
M1 Local
Ce parcours s’adresse aux étudiants francophones souhaitant étudier sur place à l’Université de Limoges. Les cours du parcours local seront dispensés en présentiel à l’Université de Limoges et en français.
M1 MIX
Ce parcours s’adresse aux étudiants francophones et anglophones souhaitant étudier sur place à l’Université de Limoges. Il s’adresse aux étudiants inscrits dans le parcours mécatronique de l’École d’ingénieurs ENSIL-ENSCI de Limoges. Trois modules de cours seront dispensés en distanciel et en anglais ; le reste de la formation est assurée à l’École d’ingénieurs ENSIL-ENSCI dans le parcours mécatronique.
M1 International
Ce parcours s’adresse aux étudiants anglophones inscrits dans une université internationale partenaire (avec la possibilité d’intégrer le parcours local en deuxième année). Huit modules de cours seront dispensés en distanciel et en anglais ; le reste de la formation est assurée dans l’université internationale partenaire.
Liste des universités partenaires :
- Université de Pise (Italie)
- Université de Quy Nhon (Vietnam)
- Université de Settat (Maroc)
- KNURE – Karkhiv National University of Radio Electronics (Ukraine)
- Faculté Polydisciplinaire de Safi de l’Université Cadi Ayyad (Maroc)
- Université Mohammed V à Rabat
M1 EUR
Ce parcours s’adresse aux étudiants francophones souhaitant étudier sur place à l’Université de Limoges. Il est adossé au parcours local mais avec une spécificité liée à l’École Universitaire de Recherche Ceramics & ICT (TACTIC Graduate School). Les cours du parcours local seront dispensés en présentiel à l’Université de Limoges et en français.
Tableaux récapitulatif des modules du M1 ACSYON
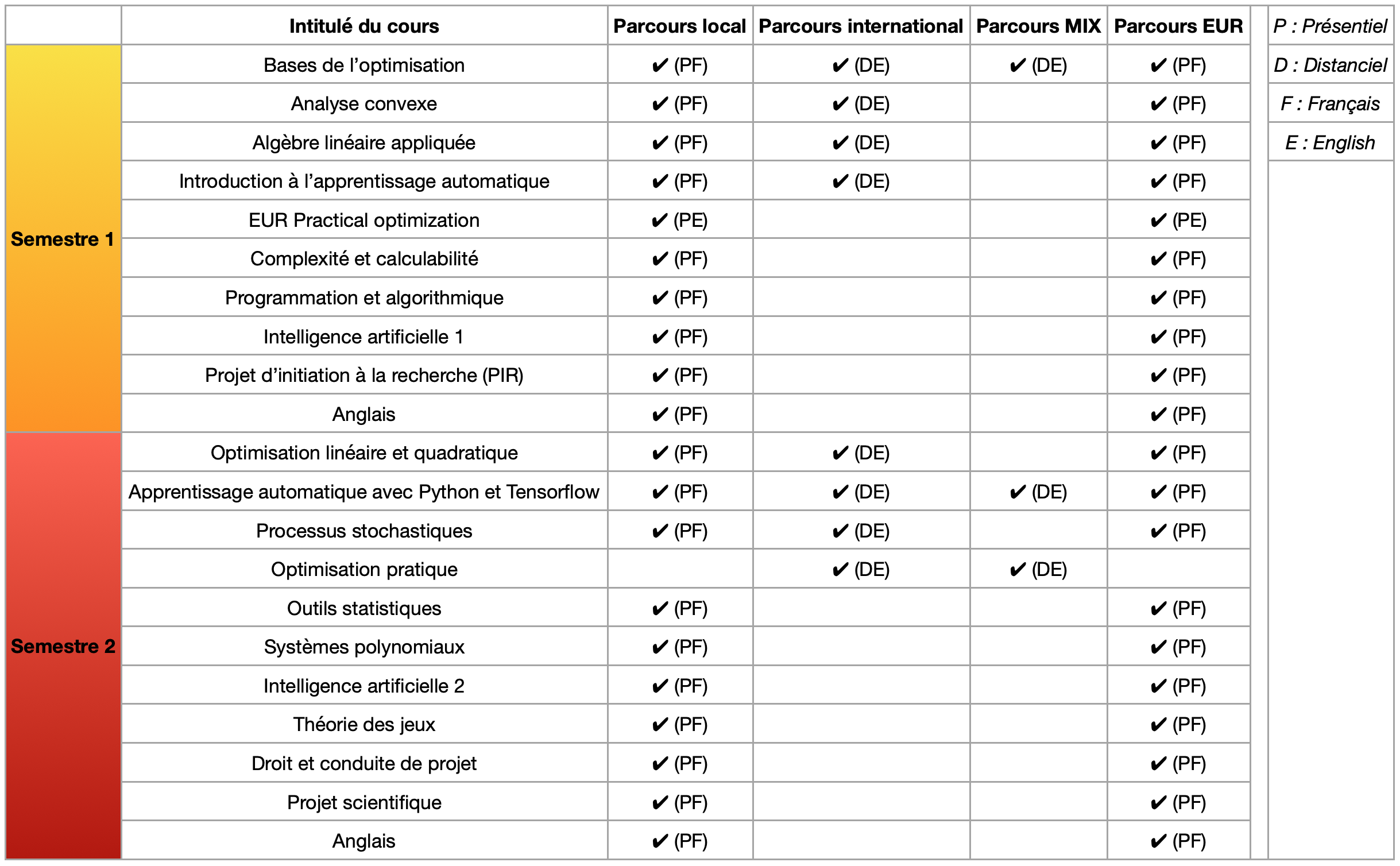
Description des cours du premier semestre
Bases de l’optimisation
Il s’agit d’un cours introductif à la théorie de l’optimisation. Nous rappelons l’optimisation à travers l’histoire, les différents problèmes d’optimisation linéaire vs non-linéaire, continue vs. discontinue, sans contraintes vs. avec contraintes, globale vs. locale, convexe vs. non-convexe, déterministe vs. stochastique. Nous démontrons les conditions d’optimalités KKT (Karush-Khun-Tucker). Nous étudions la dualité (dualité forte et faible), relation entre le problème et le dual, problèmes de complémentarités, analyse de sensibilité.
Prérequis
Algèbre linéaire, Calcul différentiel et topologie en dimension finie
Mots clé
Optimisation sans contraintes, Optimisation avec contraintes, Conditions d’optimalité, Lagrangien, dualité.
Analyse convexe
Ce module est un cours d’introduction à l’analyse convexe. Dans une première partie, nous développons les notions d’espaces affines, d’ensembles convexes et d’ensembles coniques. Nous énonçons les théorèmes de projection, de séparation et leurs applications directes. Nous aborderons également le théorème bipolaire et les théorèmes de Krein-Milman, de Minkowski et de Farkas. La deuxième partie est consacrée aux fonctions convexes et à leurs régularités. Nous introduisons la notion de sous-différentiel et de conjuguée de Fenchel. Nous terminons avec une introduction à la dualité en optimisation convexe.
Prérequis
Topologie et calcul différentiel dans R^n
Mots-clé
Ensembles convexes et coniques, théorèmes de projection et de séparation, théorème bipolaire, fonctions convexes et régularité, sous-différentiel et conjuguée de Fenchel, dualité en optimisation convexe.
Algèbre linéaire appliquée
L’objectif de ce cours est de donner un aperçu des concepts et algorithmes importants de l’algèbre linéaire appliquée, de leur analyse et de certaines de leurs applications.
Prérequis
Algèbre linéaire, Analyse numérique matricielle, espaces vectoriels normés, Algèbre bilinéaire, espaces vectoriels euclidiens, calcul différentiel dans R^n
Mots clés
Valeurs propres, valeurs singulières, normes, conditionnement, décompositions (LU, QR), décomposition en valeurs propres, décomposition en valeurs singulières.
Introduction à l’apprentissage automatique
L’apprentissage automatique est l’un des domaines clés de l’intelligence artificielle et il est utilisé dans de nombreuses technologies récentes telles que : les moteurs de recherche, la reconnaissance d’images, la reconnaissance vocale, les réseaux sociaux, les véhicules autonomes, le diagnostic médical etc ….
Elle concerne l’étude et le développement de modèles quantitatifs qui permettent à un ordinateur d’effectuer des tâches et d’apprendre par l’expérience. Ce cours est une introduction aux concepts et algorithmes fondamentaux de l’apprentissage automatique. L’essentiel du cours porte sur la conception de modèles d’apprentissage statistique et sur les algorithmes d’optimisation qui sont utilisés pour les entraîner. »
Prérequis
Algèbre linéaire, topologie et calcul différentiel dans R^n, probabilités et statistiques
Mots clés
Apprentissage supervisé, recherche des plus proches voisins, machine à vecteurs de support, réseaux de neurones artificiels
EUR Practical optimization
The goal is to learn how to effectively and numerically solve an optimization problem. We will see how to modelize an optimization problem and to write a model with the modeling language AMPL. How to choose an appropriate solver to compute an optimal solution in some concrete situations. We will review the optimality conditions of an optimization problem and see how we try to solve them in practice and what is actually solved.
Prérequis
Optimization basics, Matlab or Python
Mots clés
Numerical optimization, modeling language
Complexité et calculabilité
Modèles de calcul : machines de Turing, fonctions récursives, calcul lambda.
Calculabilité. Décidabilité.
Classe de complexité : P, NP, co-NP, problèmes NP-complets.
Complexité des algorithmes.
Mots clés
Langages, machines de Turing, classes de complexité
Programmation et algorithmique
Analyse et preuves d’algorithmes, invariants de boucle. Arithmétique élémentaire, algorithme d’Euclide, exponentiation rapide. Algorithmes de tri (insertion, fusion, bulles, quicksort) et analyse de leurs coûts. Algèbre de Boole, fonctions booléennes. Graphes (chemins eulériens, hamiltoniens, théorème des 4 couleurs). TP : Programmation en C (types, fonctions, pointeurs, makefiles). Développement d’un projet en petit groupe.
Mots clés
Algorithmes, tris, fonctions booléennes, graphes. Programmation en langage C.
Intelligence artificielle 1
Ce module offre une base solide sur les différentes méthodes d’intelligence artificielle appliquées dans des domaines aussi variés que la résolution de problèmes dans de grands espaces de recherche, la recherche de solution en situation d’advesité, la résolution de systèmes de satisfactions de contraintes ou le raisonnement incertain.
Prérequis
Algorithmique et structures de données. Notions de probabilités.
Mots clés
Algorithme A* et meilleur d’abord, recherche locale et globale, jeux à deux personnes, CSP, réseaux de Bayes.
Projet d'initiation à la recherche (PIR)
Il s’agit d’un projet en « autonomie » mais conduit sous la responsabilité d’un enseignant. La production de ce module, au Semestre 1, sera un rapport (partie d’initiation à la recherche) qui sera ensuite évalué. Pour la suite du travail (partie projet scientifique) au semestre 2, le rendu est un rapport et une soutenance.
Prérequis
Recherche, littérature, état de l’art
Anglais
English with a focus on science or on today’s most pressing topicsesl classes: the 4 major skills: oral and written comprehension, oral and written production
Description des cours du deuxième semestre
Optimisation linéaire et quadratique
Le cours consiste en une introduction à l’optimisation linéaire (LP) et quadratique (QP). Nous nous intéressons aux aspects de dualité en LP, à la méthode du simplexe pour la programmation linéaire, aux conditions de optimalité et complémentarité et aux méthodes de points intérieurs. Dans la deuxième partie du cours, nous nous intéressons à l’optimisation quadratique sans contraintes et avec contraintes linéaires de type égalité et inégalité, et à sa résolution. Nous allons traiter des exemples d’applications, notamment pour les sciences des données, la théorie des décisions et les mathématiques financières, par exemple l’optimisation de portefeuille, planification statique, problèmes de transport et conception de réseaux. Des travaux pratiques seront basés sur la programmation avec Matlab/Scilab.
Prérequis
Algèbre linéaire élémentaire et géométrie convexe.
Mots clés
Optimisation conique, dualité, conditions d’optimalité, algorithme du simplexe, méthodes de points intérieurs, solveurs numériques.
Apprentissage statistique avec Python et TensorFlow
Le but de ce cours est de traiter des exemples concret d’apprentissage statistique en utilisant le langage Python et les librairies Scikit-learn et Tensorflow. Nous commencerons par revoir les bases du langage Python ainsi que la manipulation des modules classiquement utilisé pour le calcul scientifique. Puis après avoir découvert le logiciel Tensorflow et l’avoir pris en main, nous étudierons différents exemples de modèles d’apprentissage automatiques afin de traiter des exemples pratiques.
Prérequis
Algèbre linéaire, calcul différentiel élémentaire, notions de probabilités et statistiques
Mots clés
Apprentissage statistique, Python, TensorFlow, réseau de neurones, SVM, méthode à noyaux
Processus stochastiques
Le but étant une introduction à la notion de processus stochastiques et de ses applications. Le cours commence par les notions de base de la théorie des probabilités. Nous étudions ensuite quelques résultats asymptotiques importants pour les variables aléatoires : loi forte des grands nombres et le théorème central limite. La deuxième partie du cours est consacrée à l’étude des chaînes de Markov, y compris leur comportement asymptotique en temps. Le cours sera illustré par des exemples d’applications.
Prérequis
Bases de probabilité et d’analyse.
Mots clés
Probabilités, théorèmes limites, marches aléatoires, chaînes de Markov et martingales.
Optimisation pratique
L’objectif est d’apprendre à résoudre numériquement un problème d’optimisation. Nous verrons comment modéliser un problème d’optimisation, écrire un modèle numérique, choisir un solveur approprié, essayer de calculer une solution optimale, puis comprendre les retours du solveur. Nous travaillerons essentiellement sur les conditions d’optimalité d’un problème d’optimisation. Nous rappellerons les conditions d’optimalité et comment les résoudre numériquement. Le cours est organisé en quatre parties : Introduction aux langages d’optimisation et de modélisation, Optimisation sans contrainte et problèmes des moindres carrés, Programmation linéaire, Programmation non linéaire.
Prérequis
Algèbre linéaire de base, calcul différentiel et pratique d’un langage comme Matlab ou Python.
Mots clé
Optimisation numérique, langage de modélisation, solveur d’optimisation, conditions d’optimalité.
Outils statistiques
Après une révision de la théorie des probabilités, on étudie plusieurs types de convergence de variables aléatoires (convergence presque sûre, en probabilité et en loi). Nous étudions ensuite le théorème de la limite centrale qui est à la base de la théorie de l’estimation paramétrique. Nous présentons en détail des méthodes d’estimation ponctuelle classiques telles que la méthode des moments et du maximum de vraisemblance. L’application du théorème de la limite centrale pour construire des intervalles de confiance et motivée et appliquée à plusieurs cas de figure. Le cours finit par une introduction à la théorie des tests d’hypothèse qui jouent un rôle fondamental dans les applications.
Prérequis
Bases en probabilités et en analyse
Mot-clés
Comportement limite de suites de variablés aléatoires, méthodes d’estimation paramétrique, tests d’hypothèse.
Systèmes polynomiaux
L’UE Systèmes polynomiaux est une introduction à la théorie de systèmes polynomiaux, c’est-à-dire à la résolution de systèmes d’équations polynomiales à coéfficients dans un corps de base. Les systèmes polynomiaux peuvent modéliser plusieurs phénomenes dans les applications, par exemple en robotique (characterisation de la cinématique inverse en 3D). Le cours introduit les outils de base pour la résolution de SP, notamment les bases de Groebner, l’elimination de variables par le résultant, la théorie de Sturm pour le cas à une variable.
Prérequis
Algèbre de base : définition d’anneau, corps, idéal, polynômes, matrices, déterminant.
Mots clés
Systèmes polynomiaux, bases de Groebner, résultant, discriminant, élimination, théorie de Sturm
Intelligence artificielle 2
L’objectif ce cours est de permettre aux étudiants de maîtriser les concepts fondamentaux de l’apprentissage automatique et d’appliquer ces notions à certains problèmes concrets tel que la sécurité de l’information. Puis leur faire acquérir des connaissances sur les techniques d’apprentissage supervisé et non supervisé.
Prérequis
Algorithmique et structures de données. Notions de probabilités. Notions sur les problèmes d’optimisation numérique.
Mots clés
Algorithme A* et meilleur d’abord, recherche locale et globale, jeux à deux personnes, CSP, réseaux de Bayes.
Théorie des jeux
Cette UE est une introduction à la théorie des jeux, et ses applications en informatique. On pourrait aussi l’appeler théorie de la décision interactive, car elle modélise des situations dans lesquelles plusieurs agents font des choix ayant à leur tour des effets sur les gains (ou pertes), ceux des uns affectant les gains des autres.
Mots clés
Equilibre de Nash, jeux non-coopératifs, stratégies dominantes/dominées
Droit et conduite de projet
Initiation au droit de l’Informatique: propriété intellectuelle, loi « Informatique et Libertés », Loi Godfrain, législation sur la cryptographie… ; Introduction à la conduite de projet Informatique.
Mots clés
Conduite de projet, travail collaboratif, droit de l’informatique
Projet scientifique
Il s’agit d’un projet en « autonomie » mais conduit sous la responsabilité d’un enseignant. La production de ce module, au Semestre 1, sera un rapport (partie d’initiation à la recherche) qui sera ensuite évalué. Pour la suite du travail (partie projet scientifique) au semestre 2, le rendu est un rapport et une soutenance.
Mots clés
Recherche, littérature, état de l’art
Anglais
English with a focus on science or on today’s most pressing topicsesl classes: the 4 major skills: oral and written comprehension, oral and written production



