1. Introduction

2. Loi uniforme

   1. Générateurs congruentiels
   2. Générateurs de type "Multiplication avec retenue"
   
   

3. Loi normale

   1. Introduction
   2. Simulation d'une loi normale
   
   

4. Loi multinormale

   1. Introduction
   2. Simulation d'une loi multinormale
   
   

5. Loi multi-lognormale

   1. Introduction
   2. Simulation d'une loi multi-lognormale
   
   

I. Introduction

Générer des nombres aléatoires sur ordinateur revient à créer une suite d'entiers :

où f est une fonction qui doit être choisie judicieusement pour que la répartition des nombres I_n ne puisse pas être distinguée de ce que donnerait le hasard. On parle alors de nombres pseudo-aléatoires.

La suite peut fournir M nombres aléatoires dans l'intervalle [0, M-1]. M dépend du type des entiers :

• entiers 16 bits : M = 2¹⁶ = 65 536
• entiers 32 bits : M = 2³² = 4 294 967 296 (soit plus de 4 milliards de nombres aléatoires !)

La valeur de départ I₀, appelée graine (seed), doit être fournie par l'utilisateur. La même graine donnera toujours la même suite de nombres. D'autre part, la suite se reproduit au bout d'un nombre de valeurs appelé période. Cette période doit être la plus grande possible.

Si la fonction f a été correctement choisie, chaque nombre a la même probabilité d'apparaître. On dit que les nombres aléatoires suivent une loi uniforme.

On montre que les autres lois de probabilité (binomiale, normale...) peuvent être simulées à partir de cette loi uniforme.

Nous décrirons ici des méthodes permettant de générer des nombres aléatoires répartis selon :

• une loi uniforme
• une loi normale (courbe de Gauss)
• une loi multinormale (loi normale à plusieurs variables) ou multi-lognormale

II. Loi uniforme

II.A. Générateurs congruentiels

C'est la base des générateurs implantés dans les langages de programmation. Ils sont du type :

avec b = 2¹⁶ par exemple.

Ces générateurs ont plusieurs inconvénients qui les font déconseiller dans la pratique.

II.B. Générateurs de type "Multiplication avec retenue" (Multiply With Carry, MWC)

Ces générateurs, introduits par George Marsaglia, sont du type :

a est le multiplicateur, b la base, c_n la retenue. On peut prendre c₀ = 0.

• Pour b = 2¹⁶, si a est choisi parmi les valeurs du tableau suivant, la période est (a × 2¹⁵ - 1).

  -----------------------------------------------------------
  18000 18030 18273 18513 18879 19074 19098 19164 19215 19584
  19599 19950 20088 20508 20544 20664 20814 20970 21153 21243
  21423 21723 21954 22125 22188 22293 22860 22938 22965 22974
  23109 23124 23163 23208 23508 23520 23553 23658 23865 24114
  24219 24660 24699 24864 24948 25023 25308 25443 26004 26088
  26154 26550 26679 26838 27183 27258 27753 27795 27810 27834
  27960 28320 28380 28689 28710 28794 28854 28959 28980 29013
  29379 29889 30135 30345 30459 30714 30903 30963 31059 31083
  -----------------------------------------------------------
  

  Tableau 1. Valeurs possibles du multiplicateur (a) pour un générateur MWC 16 bits.
  
• Pour b = 2³², si a est choisi parmi les valeurs du tableau suivant, la période est (a × 2³¹ - 1).

  -------------------------------------------------------
   1791398085 1929682203 1683268614 1965537969 1675393560
   1967773755 1517746329 1447497129 1655692410 1606218150
   2051013963 1075433238 1557985959 1781943330 1893513180
   1631296680 2131995753 2083801278 1873196400 1554115554
  -------------------------------------------------------
  

  Tableau 2. Valeurs possibles du multiplicateur (a) pour un générateur MWC 32 bits.

Un générateur 32 bits peut aussi être obtenu en concaténant 2 nombres de 16 bits. La période est alors égale au produit des périodes des deux générateurs.

Ces générateurs ont de meilleures propriétés que les précédents et sont donc recommandés.

III. Loi normale

III.A. Introduction

La loi normale, notée N(m, s), est caractérisée par sa moyenne m et son écart-type s (ou sa variance s²). Elle est telle que :

• 68% des valeurs sont comprises dans l'intervalle m ± s
• 95% des valeurs sont comprises dans l'intervalle m ± 2s (en fait, m ± 1.96s)
• 99,7% des valeurs sont comprises dans l'intervalle m ± 3s

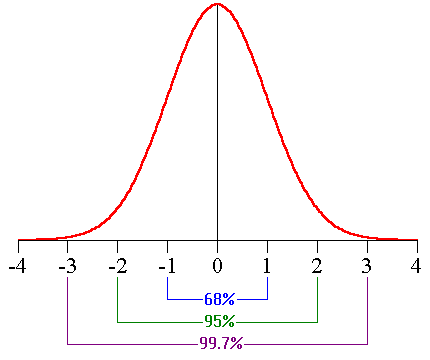
La loi N(0, 1) est appelée loi normale réduite. Elle est représentée sur la courbe suivante (courbe de Gauss) :

III.B. Simulation d'une loi normale

On utilise la méthode de Box-Muller : si x₁ et x₂ sont deux nombres aléatoires uniformes sur ]0,1[, les nombres y₁ et y₂ définis par :

suivent la loi normale réduite.

On en déduit que les nombres z₁ = m + sy₁ et z₂ = m + sy₂ suivent la loi normale N(m, s).

IV. Loi multinormale

IV.A. Introduction

La loi multinormale correspond à l'extension de la loi normale au cas de n variables x₁, x₂,... x_n. Elle est caractérisée par un vecteur de moyennes m et une matrice de variance-covariance V. On la note N(m, V).

• L'élément m_i du vecteur m représente la valeur moyenne de la variable x_i
• L'élément diagonal V_ii de la matrice V représente la variance s_i² de la variable x_i (s_i étant l'écart-type)
• L'élément non diagonal V_ij de la matrice V représente la covariance des variables x_i et x_j

  Le coefficient de corrélation r_ij s'en déduit par :

  

  Ce coefficient est toujours compris entre -1 et 1. Il est positif si x_i et x_j ont tendance à varier dans le même sens, négatif dans le cas contraire.

• La matrice V est symétrique définie positive.

IV.B. Simulation d'une loi multinormale

Pour simuler une loi multinormale N(m, V) de dimension n, on applique l'algorithme suivant :

1. Soit u un vecteur constitué de n nombres aléatoires indépendants distribués selon la loi normale réduite.
2. Soit L la matrice triangulaire inférieure résultant de la décomposition de Cholesky de la matrice V (voir cours sur le calcul matriciel).
3. Le vecteur x = m + Lu suit la loi multinormale N(m, V).

V. Loi multi-lognormale

V.A. Introduction

On dit que le vecteur x suit la loi multi-lognormale LN(m, V), où m désigne le vecteur de moyennes et V la matrice de variance-covariance, si le vecteur x° tel que :

suit une loi multinormale.

V.B. Simulation d'une loi multi-lognormale

Si x suit la loi multi-lognormale LN(m, V), de dimension n, on définit la variable auxiliaire x° distribuée selon la loi multinormale L(m°, V°) telle que :

Le vecteur x tel que x_i = exp(x°_i) suit alors la loi multi-lognormale LN(m, V).